Inhaltsverzeichnis
Maxima
Hier werden die Basics von STACK und insbesondere Maxima in Moodle zusammengefasst. Originaltexte zusammengetragen und übersetzt aus https://github.com/maths/moodle-qtype_stack/tree/master/doc/en/CAS und der Dokumentation "Minimal Maxima".
STACK arbeitet im Hintergrund mit dem Computeralgebrasystem Maxima. Dies bedeutet, in STACK-Aufgaben können generell Maxima Funktionen und Berechnungen durchgeführt werden, wobei es einige Einschränkungen in STACK gibt. Weiterhin gibt es Funktionen die nur in STACK und nicht in Maxima definiert sind. Welche Funktionalitäten zur Verfügung stehen, kann man hier nachschlagen.
Objekte
Objekte in Maxima sind Ausdrücke (englisch: expressions). Diese kommen generell in drei Formen vor:
- Atome wie Symbole, Strings und Zahlen
- Operatoren mit ihren Argumenten (die wiederum Operatoren oder Atome sein können)
- Mathematische Ausdrücke die mathematische Operatoren (+-*/<>=) oder Funktionen (z.B. sin(x)) enthalten
Die wichtigsten Objekte sind
- Gleichungen
- Ungleichungen
- Sets (z.B.
A:{1,2}) - Listen (z.B.
L:[1,2,3]mit Zugriff auf x-tes Element durch BefehlL[x]) - Matrizen (z.B.
M:matrix([1,2],[3,4])mit jede Zeile als eigene Liste und Zugriff durchM[x][y]) - logische Ausdrücke, verknüpft mit logischem and oder or (z.B.
x=1 or x=2) - (sonstige) Ausdrücke
Listen
Listen können z.B. angelegt werden mit:
L:[1,2,3];
Es wird also der Variable L die Liste [1,2,3] zugeordnet. Dementsprechend kann mit
L[i];
auf das i-te Element der Liste zugegriffen werden. Das erste Element der Liste ist somit entsprechend L[1]. Erwähnenswert ist hier noch, dass eine Liste auch weitere Listen enthalten kann. In einer Liste L die [[1,true],[2,true],[3,false]] enthält, kann man also mit
L[3][2];
auf das zweite Element in der dritten Liste zugreifen (in diesem Fall false). Eine weitere nützliche Operation ist
map(f, L);
Hiermit wird f auf jedes Element von L angewandt. Möchte man jedes Element in der Liste aufaddieren, so kann man dies mit
apply("+",L);
tun. Eine weitere Operation ist
for x in L do ex;
Dies wendet die Operation ex für jedes Element von L an, wobei x in ex als Variable genutzt werden kann. Weiterhin kann man mit
length(L);
die Anzal der Elemente in L bestimmen.
Matrizen
Matrizen können mit
M:matrix(L1, ..., Ln);
angelegt werden, wobei L1 bis Ln Listen sind, die die Zeilen der Matrix repräsentieren. Mit den Befehlen
M[i,j]
oder
M[i][j]
greift man auf das Element in der i-ten Zeile und j-ten Spalte zu. Der Befehl
M:zeromatrix(n,m);
erzeugt direkt eine n x m - Nullmatrix.
Die Matrixmultiplikation wird mit dem Punkt als Operator durchgeführt. Das heißt M.L, L.M und M.N sind Matrixmultiplikationen, mit L als Liste und M und N als Matrizen.
Weitere nützliche Funktionen für Matrizen:
| Funktion | Output |
|---|---|
transpose(M) | Transponiert die Matrix M. |
eigenvalues(M) | Eigenwerte von M. |
eigenvectors(M) | Eigenvektoren von M. |
length(M) | Anzahl der Zeilen von M. |
length(transpose(M)) | Anzahl der Spalten von M. |
Sets/Mengen
Sets erstellt werden mit
A:set(a,b,c,...);
oder mit
A:{a,b,c,...};
Hier sind a,b,c,… die Elemente des Sets.
Beide Alternativen sind äqivalent.
In Sets erscheinen die Elemente des Sets nur einmal.
Das heißt
A:set(a,b,c,b,a);
liefert das Set {a,b,c}.
Ist dies nicht der Fall, so ist wahrscheinlich die Simplifikation(siehe Abschnitt zu Simplifikation) nicht aktiviert.
Diese kann man aber aktivieren indem man Aufgabenweites Simplify in den Optionen der STACK-Frage auf Ja setzt, indem man die simp Variable temporär in den Aufgabenvariablen auf true setzt
simp:true; A:set(a,b,c,b,a); simp:false;
oder indem man die Funktion ev() nutzt.
A:ev(set(a,b,c,b,a), simp);
Nützliche Funktionen für Sets:
| Funktion | Output |
|---|---|
union(A,B) | Vereinigung der beiden Mengen A und B. |
intersect(A,B) | Schnitt der Mengen A und B. |
cardinality(A) | Mächtigkeit der Menge A. |
Zuweisungen
| Input | Resultat |
|---|---|
a:1 | Der Variable a wird der Wert 1 zugewiesen. |
a=1 | Eine Gleichung, die noch zu lösen ist. |
f(x):=x^3 | Definition einer Funktion. |
Innerhalb Zuweisungen können Maxima-Funktionen genutzt werden.
Beispiel:
a:expand((x+1)*(x-5));
Funktionen definieren
Um eine Funktion zu defnieren gibt es zwei Möglichkeiten. Eine ist der Operator := und die zweite ist die Funktion define(). Die erstere haben wir bereits im vorangehenden Kapitel gesehen.
- Die erste Möglichkeit ist eine Funktion mit dem Operator
:=zu definieren. So kann man z.B. eine Funktionfoo(x)definieren mitfoo(x) := diff(x^2 + x + 5, x). Unterfoo(x)ist nun die Funkiondiff(x^2 + x + 5, x)hinterlegt. Hier wird nun bei jedem Aufruf vonfoo(x)die Funktionx^2 + x + 5nachxdifferenziert und der übergebene Wert an der Stellexeingesetzt. Es ist eventuell nicht gewollt, bei jedem Aufruf die Funktion erneut zu differenzieren, daher gibt es noch eine zweite Möglichkeit Funktionen zu definieren. - Es ist auch möglich eine Funktion mit der Maxima Funktion
define()zu definieren. Mitdefine(foo(x), diff(x^2 + x + 5, x))wird direkt beim Definieren der Funktiondiff()ausgeführt und so ist letzten Endes die Funktion2*x + 1unterfoo(x)hinterlegt.
Gleichungen lösen
Gleichungen können mit der Funktion solve(ex, x) gelöst werden.
solve(x^2 + x - 30 = 0, x);
löst die Gleichung x^2 + x - 30 = 0 nach x auf und gibt die Liste
[x = -6, x = 5]
aus, die die Lösungen enthält.
Ist ex keine Gleichung, so wird ex = 0 angenommen.
Auch Gleichungssysteme können mit solve([ex1, …, exn], [x1, …, xn]) gelöst werden.
solve([x + y = 0, x - y = 10], [x, y]);
liefert als Ergebnis
[[x=5, y=-5]]
Hierbei ist zu beachten, dass die Lösung eine Liste innerhalb einer Liste ist. Dies liegt daran, dass jede mögliche Lösung als eigene Liste aufgelistet wird.
Integrieren und Differenzieren
Mit Hilfe von Maxima kann man mit Hilfe von Funktionen sehr einfach Integrale berechnen lassen und differenzieren.
Integrieren
Es können mit integrate(ex, x) uneigentliche und mit integrate(ex, x, a, b) eigenliche Integrale ausgewertet werden, wobei ex die zu integrierende Funktion beschreibt, x die Variable und a und b die Grenzen definieren.
So liefert z.B.
integrate(1/(1+x), x);
entsprechend das Ergebnis
ln(|x+1|)
Einige Maxima Funktionen können beim Integrieren sehr nützlich sein.
Möchte man das eben genannte Integral zwischen den Grenzen 0 und a berechnen, so sollte man vorher angeben, dass a größer 0 ist.
Dies kann man vor dem Integrieren mit dem Befehl
assume(a>0);
erreichen. Andernfalls würde
integrate(1/(1+x), x, 0, a);
zu Fehlermeldungen führen.
Möchte man das Integral nicht ausrechnen, sondern einfach nur als Integral ausgeben, so kann man dies mit einem Apostroph vor dem Befehl erreichen, was die Ausführung der Funktion in Maxima unterdrückt, also z.B.
'integrate(1/(1+x), x, 0, a);
Möchte man diesen Ausdruck dann doch integrieren kann man das mit dem Befehl
ev(ex, integrate);
tun. Wird auch ohne das Apostroph nur das Integral angezeigt, so konnte kein Integral gefunden werden und man muss eventuell manuell mit Substiution nach einer Lösung suchen.
Differenzieren
Einfaches differenzieren einer Funktion ex nach Variable x funktioniert mit dem Befehl
diff(ex, x);
Die n-te Ableitung erhält man mit
diff(ex, x, n);
Mit
diff(ex, x_1, n_1, x_2, n_2, ..., x_m, n_m);
wird ein Ausdruck ex zunächst n_1 mal nach x_1 differenziert, dann n_2 mal nach x_2 differenziert, etc.
Auch hier kann man genauso wie beim Integrieren, die tatsächliche Berechnung durch ein vorgestelltes Apostroph unterbinden (z.B. 'diff(x^2, x)).
Prädikat-Funktionen
Funktionen in STACK/Maxima die als Input einen Ausdruck nehmen und true oder false ausgeben.
ex steht für den Ausdruck (expression).
Beachte: Jeder Name einer Prädikats-Funktion endet auf „p“.
| Funktion | Output |
|---|---|
floatnump(ex) | Überprüft ob ex ein float ist. |
numberp(ex) | Überprüft ob ex eine Zahl ist. Wobei Symbole wie \sqrt(2), \pi oder i nicht als Zahlen gewertet werden. |
real_numberp(ex) | Überprüft ob ex eine reele Zahl ist (schließt irrationale Zahlen und symbolische Zahlen wie \pi mit ein. |
setp(ex) | Überprüft ob ex ein Set ist. |
listp(ex) | Überprüft ob ex eine Liste ist. |
matricep(ex) | Überprüft ob ex eine Matrix ist. |
polynomialp(ex,[v]) | Überprüft ob ex ein Polynom in der Liste der Variable v ist. |
equationp(ex) | Überprüft ob ex eine Gleichung ist. |
functionp(ex) | Überprüft ob ex eine Funktion ist, definiert durch den Operator :=. |
inequalityp(ex) | Überprüft ob ex eine Ungleichnung ist. |
expressionp(ex) | Überprüft ob ex keine Matrix, Liste, Set, Gleichung, Funktion oder Ungleichung ist. |
polynomialsimpp(ex) | Überprüft ob ex ein Polynom in seinen eigenen Variablen ist. |
simp_numberp(ex) | Überprüft ob ex eine Zahl ist falls simp:false. |
simp_integerp(ex) | Überprüft ob ex ein Integer ist falls simp:false. |
real_numberp(ex) | Überprüft ob ex eine reelle Zahl ist. |
rational_numberp(ex) | Überprüft ob ex eine rationale Zahl ist. |
lowesttermsp(ex) | Überprüft ob ein Bruch ex nicht mehr kürzbar ist. |
element_listp(ex,l) | true wenn ex ein Element der Liste l ist. (Sets haben elementp, Listen jedoch nicht) |
all_listp(p,l) | true wenn alle Elemente von l die Bedingung p erfüllen. |
any_listp(p,l) | true wenn zumindest ein Element von l die Bedingung p erfüllt. |
sublist(l,p) | Gibt eine Liste mit den Elementen aus l zurück die die Bedingung p erfüllen. |
expandp(ex) | true wenn sich ex in seiner aufgelösten Form befindet. |
factorp(ex) | true wenn sich ex in seiner faktorisierten Form befindet. |
continuousp(ex,v,xp) | true wenn ex stetig ist in Bezug auf v an der Stelle xp. |
diffp(ex,v,xp,[n]) | true wenn ex (optional n mal) nach v differenzierbar ist an der Stelle xp (unreliable). |
rationalized(ex) gibt zudem false zurück, falls der Ausdruck ex Brüche enthält, die im Hauptnenner z.B. Wurzelausdrücke enthalten mit einer Liste der Funde und true sonst. Ist aber an sich keine Prädikats-Funktion.
Zahlen
| Konstanten | |
|---|---|
| %e | Eulersche Zahl |
| %pi | Kreiszahl |
| %i | imaginäre Einheit |
| %phi | Goldener Schnitt |
Manche Zahlen wie z.B. e oder pi sind schon automatisch als Variablen angelegt. Das heißt pi: %pi ist nicht notwendig. Möchte man jedoch pi nur als Symbol und nicht als Zahl benutzen so kann man den Befehl stack_reset_vars(true) mit in die Aufgabenvariablen aufnehmen.
Gleitkommazahlen
Mit der Funktion float(ex) kann aus ex eine Gleitkommazahl gemacht werden. Mit rat(ex) kann ex „rationalisiert“ werden. Für
rat(0.25);
erhalten wir entsprechend den Bruch 1/4 als Output.
Aufpassen muss man, wenn Ausdrücke wie 2e5 (im Sinne von 2 x 10^5) benutzt werden sollen, da wie oben schon beschrieben e als Eulersche Zahl angelegt wird. Hier muss man die strikte Syntax in Fragen aktivieren, da sonst der Ausdruck 2e5 als 2*e*5 interpretiert wird.
Runden
Gerundet wird standardmäßig in STACK mit
round(x);
wobei hier zu beachten ist, dass das symmetrische Runden genutzt wird. Es wird also bei .5 auf die nächste gerade Zahl gerundet. Das heißt, 2.5 wird auf 2 abgerundet und 3.5 auf 4 aufgerundet. Kaufmännisches Runden kann dennoch mit der Funktion
significantfigures(x, n);
erreicht werden.
Zufallswerte
Einfache Zufallswerte
Die Maxima Funktion random() erzeugt Zufallszahlen, jedoch sollte dies nicht für STACK-Aufgaben genutzt werden, denn dies verursacht, dass ein Student, der eine Frage ein weiteres Mal ansieht, neue Zufallswerte erhält.
Um dies zu vermeiden, wurde für STACK eine Funktion rand(), mit festgesetztem seed, definiert.
Diese ist also dementsprechend für STACK zu bevorzugen.
| Funktion | Output |
|---|---|
rand(n) | Erzeugt eine Zufallszahl zwischen 0 und n-1. |
rand(n.0) | Erzeugt eine zufällige Gleitkommazahl zwischen 0 und n. |
float(rand(2000)/1000) | Erzeugt eine Zufallszahl zwischen 0 und 2 mit drei Nachkommastellen (indem zuerst mit rand(2000) eine Zahl zwischen 0 und 1999 erzeugt wird und diese mit dem Teilen durch 1000 um drei Nachkommastellen verschoben wird). Die Werte können hier natürlich nach Belieben angepasst werden. |
rand([a, b, …, z]) | Zieht ein zufälliges Element aus der Liste [a, b, …, z]. |
rand(matrix(…)) | Wendet die Funktion rand() auf jedes Element der Matrix an. |
Es ist ratsam beim Erzeugen von Zufallszahlen keine bedingte Anweisungen wie z.B. if zu benutzen sondern auf einfachere Mittel zurückzugreifen.
Möchte man beispielsweise eine Zufallszahl erzeugen, die eine kleine Primzahl ist, dann ist der Ausdruck
rand([2, 3, 5, 7, 11, 13, 17, 19]);
vielleicht nicht die schönste, aber dafür die zuverlässigste Variante.
Weiterer Tipp: Möchte man Zufallszahlen nicht ab 0 aufwärts sondern z.B. zwischen -5 und 10 oder zwischen 11 und 42 erzeugen, so kann man dies mit der Kombination von Zufallswerten und der Addition oder Substraktion von festen Werten erreichen.
Zufallswerte zwischen 11 und 42:
p: rand(32)+11;
Matrix mit Zufallswerten zwischen -5 und 10:
A: rand(matrix([16,16],[16,16]))-matrix([5,5],[5,5]);
Weitere Funktionen zum Erzeugen von Zufallswerten
| Funktion | Output |
|---|---|
rand_with_step(lower, upper, step) | Zieht eine Zufallszahl aus dem Set {lower, lower+step, lower+2*step, …, final}, wobei final ⇐ upper und final+step > upper. |
rand_range(lower, upper, step) | Das Gleiche wie bei rand_with_step(lower, upper, step). |
rand_with_prohib(lower, upper, list) | Erzeugt eine Zufallszahl zwischen lower und upper, aber schließt dabei alle Elemente aus list aus. |
rand_selection(ex, n) | Erzeugt eine Liste mit n Zufallswerten ohne Zurücklegen aus der Liste ex. |
random_permutation(ex) | Gibt eine zufällige Permutation der Liste ex zurück. |
Beispiele
Zufallszahl aus {-5, -2, 1}:
a: rand_with_step(-5, 3, 3);
Zufallszahl aus {-5, -4, -3, 3, 4, 5}:
b: rand_with_prohib(-5, 5, [-2, -1, 0, 1, 2]);
Diese Funktion ist z.B. nützlich um bei Brüchen zu vermeiden durch 0 zu teilen.
Drei zufällige Elemente aus [1, 2, 3, 4, 5] ziehen:
c: rand_selection([1, 2, 3, 4, 5], 3);
Folgender Befehl könnte beispielsweise [4, 3, 5, 1, 2] liefern:
d: rand_permutation([1, 2, 3, 4, 5]);
Erzeugen eines Polynoms vierten Grades mit zufälligen Koeffizienten zwischen 0 und 6:
polynom: apply("+", makelist(rand(7)*x^k, k, 0, 4))
Hier wird zunächst mit makelist(ex, k, i, j) eine Liste erstellt, die aus den Elementen ex besteht, wobei jeweils die Variable k in ex mit den Zahlen zwischen i und j ersetzt wurde.
Die Koeffizienten sind randomisiert und mit apply(„+“, ex) werden schließlich die Listenelemente aufaddiert, so dass wir ein Polynom erhalten.
Fragentext:
Ein Pendel befindet sich auf dem Planeten {@p@}. Welche Länge muss das Pendel besitzen um eine Periode von {@t@}s zu haben?
Aufgabenvariablen:
t:rand(5)+3; idx:rand(3)+1; /* Index bei Listen starten bei 1, rand(n) liefert 0,...,n-1. */ l1:["Merkur", "Erde", "Mars"]; l2:[3.61, 9.8, 3.75]; p:l1[idx]; ta:t*l2[idx]/(4*%pi^2);
STACK spezifische Funktionen
Folgende Funkionen sind nur in STACK und nicht Maxima definiert:
| Funktion | Output |
|---|---|
significantfigures(x, n) | Rundet die Zahl x an der n-ten Stelle der Zahl. |
decimalplaces(x, n) | Rundet die Zahl x käufmännisch auf die n-te Nachkommastelle. |
commonfaclist(l) | Gibt den größten gemeinsamen Faktor der Zahlen in der Liste l zurück. |
list_expression_numbers(ex) | Erstellt eine Liste aus den Elementen von ex, für die gilt numberp(ex) = true. |
Vereinfachen und Ordnen
Terme ordnen
Als Voreinstellung ordnet Maxima Terme automatisch in umgekehrter lexikographischen Ordnung an. Also würde man z.B. eine Variable mit dem Term a+b+c belegen und diese im Fragetext ausgeben, so erscheint als Output automatisch c+b+a.
Die Ordnung kann man mit den Befehlen
ordergreat(v_1, v_2, ..., v_n);
oder
orderless(v_1, v_2, ..., v_n);
geändert werden. Dabei würde die Ordnung v_1 > v_2 > … > v_n bzw. v_1 < v_2 < … < v_n angenommen werden.
Das heißt bei einer Eingabe von
ordergreat(a, b, c)
erhält man im obigen Beispiel einen Output von a+b+c.
Logarithmus
| Funktionen | |
|---|---|
log(x) | Natürlicher Logarithmus (Basis e). |
lg(x) | Logarithmus von x zur Basis 10. |
lg(x, n) | Logarithmus von x zur Basis n. |
Selektive Simplifikation
In STACK-Aufgaben kann man in den Optionen des Potential response tree die globale Variable simp ändern. Dies geschieht unter dem Optionspunkt Auto-Vereinfachung. Es wird dementsprechend die Variable simp auf true oder false gesetzt. Dies kann man auch manuell tun mit dem Befehl simp:true.
Is diese Variable auf false gesetzt, so werden Terme wie 4+5 von Maxima nicht automatisch zu 9 vereinfacht, sondern so belassen.
Ist simp:false gesetzt, so kann mit ev(ex, simp) ein Ausdruck ex mit Vereinfachung ausgewertet werden.
Plots
Möchte man in einer STACK-Aufgabe plotten, so muss man aufpassen, in welche Dokumentationen man schaut.
Obwohl STACK mit dem CAS Maxima operiert, können vor allem in diesem Themengebiet nicht die gleichen Funktionen wie in Maxima benutzt werden.
In Maxima existieren allgemein Funktionen wie plot2d() und plot3d() mit denen man wunderschöne plots und Grafiken erstellen kann.
In Moodle existieren diese nicht.
Es wurde eine neue Funktion plot() angelegt, die ausgewählte Funktionalitäten von plot2d() enthält.
Wie man die plot() Funktion nutzen kann und was im Vergleich zu plot2d() möglich oder nicht möglich ist, werden wird in diesem Kapitel weiter erläutert.
plot()
Zur Erklärung der Plotfunktion in STACK zunächst ein einfaches Beispiel:
plot(x^2,[x,-5,5])
Hier wird ein plot der Funktion x^2 im Bereich -5 < x < 5 erzeugt.
y-Achse anpassen
Die y-Achse kann man folgendermaßen festlegen:
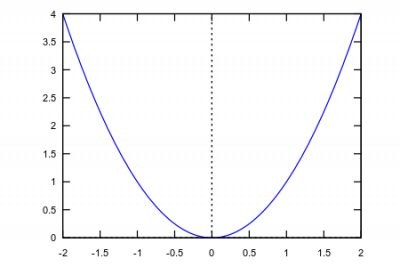
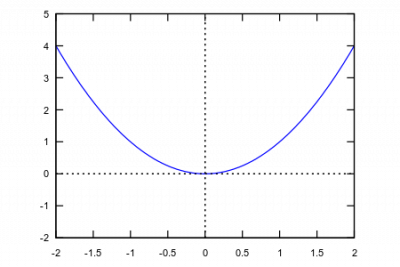
plot(x^2,[x,-5,5],[y,-2,5])
Also in diesem Fall von -2 bis 5. Dies funktioniert aber nicht immer problemlos in STACK.
Mehrere Funktionen in einer Grafik
Mehrere Funktionen kann man mit Hilfe einer Liste in der selben Grafik ausgeben:
plot([x^2,sin(x)],[x,-1,1])
Tradionelle Axen
Traditionelle Axen, die nicht in Kastenform angezeigt werden können mit dem folgenden Einstellungen der plot() Funktion erzeugt werden:
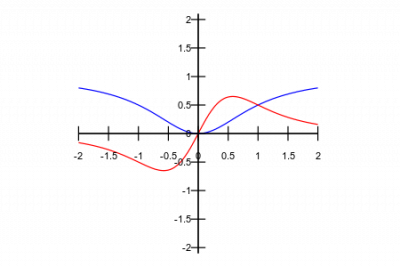
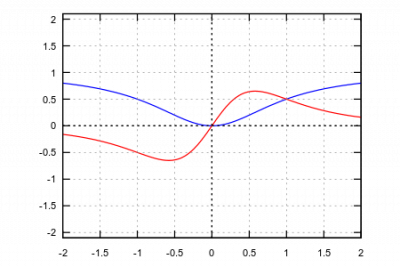
plot([x^2/(1+x^2), 2*x/(1+x^2)^2], [x, -2, 2], [y, -2.1, 2.1], [box, false], [yx_ratio, 1], [axes, solid], [xtics, -2, 0.5, 2], [ytics, -2, 0.5, 2])
Beschriftungen
Beschriftungen von z.B. Achsen können generell mit den Befehlen bzw. Optionen ylabel und xlabel eingefügt werden (konkretes Beispiel hierfür folgt weiter unten).
Die ylabel Option rotiert jedoch die Beschriftung um 90 Grad.
Möchte man eine horizontale Beschriftung der y-Achse einfügen so kann die Option label genutzt werden, wie man im folgenden Beispiel sehen kann:
plot([x^2/(1+x^2),2*x/(1+x^2)^2], [x, -2, 2], [y,-2.1,2.1], [label,["y",-2.5,0.25]])
Hier wird an der Koordinate (-2.5, 0.25) die Beschriftung „y“ der Grafik hinzugefügt. So kann man natürlich auch beliebig Beschriftungen innerhalb der Grafik einfügen und somit auch z.B. Funktionen oder Punkte beschriften.
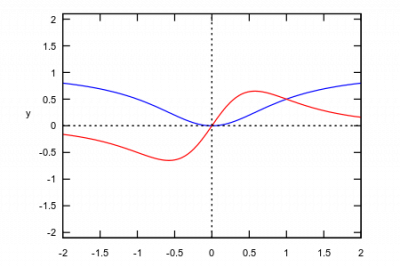
Koordinatennetz
Um ein Koordinatennetz in einer Grafik zu hinterlegen, kann die Option grid2d benutzt werden.
plot([x^2/(1+x^2),2*x/(1+x^2)^2], [x, -2, 2], [y,-2.1,2.1], grid2d)
In STACK unterstützte Optionen für Plots
Hier eine Liste aller Optionen die von plot() in STACK und damit in Moodle unterstützt werden:
| Option | |
|---|---|
xlabel | Beschriftung für die x-Achse. |
ylabel | Beschriftung für die y-Achse. |
label | Beschriftung an einer bestimmten Stelle in der Grafik einfügen. |
legend | Legende anzeigen für Funktionen. |
color | Farben von einzelnen Funktionen ändern. |
style | Plotstil festlegen. |
point_type | Punktstil festlegen. |
nticks | Anzahl der Stützstellen zur Kurvenberechnung. |
logx | Logarithmische Skalierung der x-Achse. |
logy | Logarithmische Skalierung der y-Achse. |
axes | Bestimmt welche Axen angezeigt werden. |
box | Bestimmt ob es einen Rahmen für die Grafik gibt. |
plot_realpart | Bei komplexen Funktionen wird nur Realteil gezeichnet. |
yx_ratio | Verhätnis von x und y-Achse. |
xtics | Festlegung der Skalenpunkte auf der x-Achse. |
ytics | Festlegung der Skalenpunkte auf der y-Achse. |
ztics | Festlegung der Skalenpunkte auf der z-Achse. |
grid2d | Koordinatennetz anzeigen. |
alt | Alternativer Text für die erstellte Grafik. |
Auswahlmöglichkeiten für Plotstil, Punktstil und Farben
style:
lines (für Linienabschnitte), points (für isolierte Punkte), linespoints (für Linienabschnitte und Punkte), oder dots
color:
red, green, blue, magenta, cyan, yellow, orange, violet, brown, gray, black, white
point_type:
bullet, circle, plus, times, asterisk, box, square, triangle, delta, wedge, nabla, diamond, lozenge
Alternativer Text für eine Grafik
Für einige erstellte Aufgaben kann es sinnvol sein den zugeordneten Text der Grafik selbst zu ändern.
Besteht die Aufgabe beispielsweise darin, dass ein Student vom Verlauf der Funktion zuordnen soll um welche Funktion es sich handelt, so könnte er dies in den Bildeigenschaften einfach nachschauen.
Ein Standardtext für eine solche Grafik lautet z.B. „STACK auto-generated plot of [x^2] with parameters [[x,-2,2],[y,-2.1,2.1]]“.
Um dies zu vermeiden, kann mit der alt Option dieser Text geändert werden.
plot(x^2,[x,-2,2],[alt,"These aren't the functions you're looking for."])
Diskrete Funktionen
Einfache diskrete Funktionen kann man mit dem Befehl discrete[[x_1, y_1],…,[x_n, y_n]] darstellen.
Beispiel:
plot([discrete,[[0,0],[1,1],[0,2]]]);
Dies ergibt den folgenden Graphen:
Diese Funktionen können wie in den Beispielen zuvor auch mit anderen Funktionen in Grafiken kombiniert werden.
Beispiele für Plots
Verschiedene Punktstile und Farben
plot([[discrete, [[10, .6], [20, .9], [30, 1.1], [40, 1.3], [50, 1.4]]], [discrete, [[11, .5], [15, .9], [25, 1.2], [40, 1.3], [50, 1.4]]]], [style,points], [point_type,circle,square], [color,black,green]);
Beschriftungen der Achsen und Legende
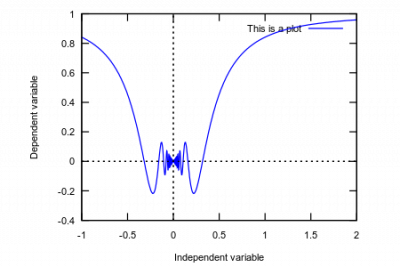
plot(x*sin(1/x),[x,-1,2],[xlabel,"Independent variable"],[ylabel,"Dependent variable"],[legend,"This is a plot"]);
Parameterdarstellung
r: (exp(cos(t))-2*cos(4*t)-sin(t/12)^5); p: plot([parametric, r*sin(t), r*cos(t), [t, -8*%pi, 8*%pi]]);
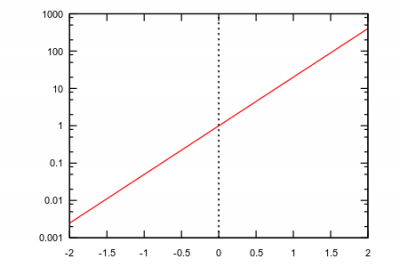
Logarithmische Skala für die y-Achse mit roter Farbe
Axen und Rahmen ausstellen
Normale Einstellung:
plot([parametric, (exp(cos(t))-2*cos(4*t)-sin(t/12)^5)*sin(t), (exp(cos(t))-2*cos(4*t)-sin(t/12)^5)*cos(t), [t, -8*%pi, 8*%pi]], [nticks, 100]);
Ohne Axen und Rahmen:
plot([parametric, (exp(cos(t))-2*cos(4*t)-sin(t/12)^5)*sin(t), (exp(cos(t))-2*cos(4*t)-sin(t/12)^5)*cos(t), [t, -8*%pi, 8*%pi]], [nticks, 100], [axes,false], [box,false]);
Abschnittsweise definierte Funktionen
Eine abschnittsweise definierte Funktion kann mit der if Anweisung definiert werden.
f0:x^3; f1:sin(x); x0:2; pg1:if x<(x0-1/1000) then f0 else if x<(x0+1/1000) then 5000 else f1;
Achtung: An plot() müssen Ausdrücke und nicht Funktionen übergeben werden, also nutzen wir f0:x^3 und nicht f(x):=x^3.
Die Werte (x0-1/1000) und (x0+1/1000) sorgen dafür, dass eine kleine Lücke im Grafen entsteht.
Nun können im CASText der plot ausgegeben werden:
{@plot(pg1,[x,(x0-5),(x0+5)],[y,-10,10])@}
Um die Endpunkte einzurkreisen kann die Aufgabe folgendermaßen erweitert werden:
f0:x^3 f1:sin(x) x0:2 pg1:if x<(x0-1/1000) then f0 else if x<x0+1/1000 then 5000 else f1; ps:[style, lines, points, points]; pt:[point_type, circle, circle, bullet]; pc:[color, blue, red,blue];
Mit zugehörigem Aufgabentext:
{@plot([pg1, [discrete,[ [x0,ev(f0,x=x0)], [x0,ev(f1,x=x0)]]], [discrete,[ [x0,ev((f0+f1)/2,x=x0)]]] ], [x,(x0-5),(x0+5)], [y,-10,10], ps, pt, pc)@}
HTML
Ist eine Grafik bereits vorhanden, so kann diese natürlich einfacher die Bilddatei auf einer Internetplattform hochzuladen und per HTML mit der entsprechenden URL direkt in den Aufgabentext einzubinden.
Von STACK nicht unterstützt
Nicht unterstützt sind folgende Eigenschaften und Funktionalitäten:
- Das
drawPaket - Die
implicit_plot()Funktion - Die
plot2d()undplot3d()Funktionen
Sonstiges
Kommentare
Nützlich für die Bearbeitung und Erstellung von Fragen, sind natürlich auch Kommentare. Zum einen um für eigene Zwecke zu dokumentieren, was gewisse Eingaben tun, aber auch damit andere wissen, was dort getan wurde.
Im Textfeld für Aufgabenvariablen können Kommentare geschrieben werden mit
/* Dieser Satz wird vom CAS ignoriert */ /* Es können auch mehrere Sätz auskommentiert werden. Somit können einfach auch ganze Kommentarblöcke geschrieben werden. So wie dieser hier. */
Im Fragentext, der für die Studenten erscheint, können Kommentare mit einem Kommentarblock eingefügt werden.
[[comment]] Diesen Kommentar werden Studenten in ihrere Frage nicht sehen. [[/comment]]
wxMaxima und Maxima Sandbox
wxMaxima
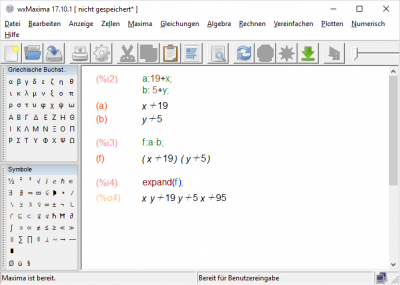
Es ist teilweise, durch immer wieder erneutes Eingeben, Speichern und Anzeigen der Fragenvorschau, sehr umständlich neue Aufgabenstellungen zu verfassen, Maxima Funktionen zu testen oder Fehler in der Aufgabenimplementierung zu finden. Daher ist es ratsam auf dem eigenen Rechner wxMaxima zu installieren, um dort mit Maxima Befehlen herumspielen zu können. wxMaxima ist ein Programm, das eine grafische Benutzeroberfläche, Menüs und Dialoge bietet um Maxima Code auszuführen.
Man kann Maxima und wxMaxima zusammen herunterladen unter: https://sourceforge.net/projects/maxima/
Befehle können in wxMaxima mit Shift + Enter ausgeführt werden. Um jedoch tatsächlich alle Funktionen von Maxima nutzen zu können, die auch in STACK vorhanden sind, braucht man die Maxima Sandbox. Dazu mehr im nächsten Abschnitt.
Maxima Sandbox
Mit Maxima und wxMaxima alleine kann man zwar Maxima Funktionen und Operationen durchführen, doch nicht alle Funktionen, die in Maxima verfügbar sind, sind (aus Sicherheitsgründen) auch in Moodle bzw. STACK verfügbar. Zudem gibt es Funktionen, die in STACK nutzbar sind, aber so nicht in Maxima existieren.
Um wxMaxima so einzurichten, dass sich das Programm wie in Moodle/STACK verhält, brauchen wir die Maxima Sandbox. Diese kann unter folgendem Link heruntergeladen werden: stack.zip
Dieses Archiv muss dann in einem Ordner namens C:\maxima_tmp\stackroot extrahiert werden und die Datei C:\maxima_tmp\stackroot\stack\sandbox.wxm mit wxMaxima geöffnet werden.
Man kann das Archiv auch in einem anderen Ordner extrahieren und muss dann nur in der sandbox.wmx die entsprechenden Pfade korrigieren.
Zum Starten der Sandbox den Cursor in den Bereich zwischen
/* No trailing slash. */ maximaplatform:...
und
print(sconcat("[ STACK-Maxima started, library version ", stackmaximaversion, " ]"))$
setzen und Strg + Enter drücken.
Als guter Test eignet sich die Funktion
rand_with_step(5,10,1);
Diese wird, bevor die Sandbox gestartet wurde, beim Drücken von Strg + Enter erst einmal nur wiederholt ausgegeben. Nach dem Start der Sandbox liefert sie eine zufällige Zahl zwischen 5 und 10.
Die offizielle Dokumentation zur Sandbox befindet sich unter https://github.com/maths/moodle-qtype_stack/blob/master/doc/en/CAS/STACK-Maxima_sandbox.md.
10 minute wxMaxima Tutorial
Um den Einstieg in die Funktionalitäten von wxMaxima zu erleichtern, kann sich auf der Website von wxMaxima ein kleines Tutorial heruntergeladen werden. Einen Link dorthin finden Sie hier: wxMaxima Dokumentation
Den direkten Link zum Download der deutschen Version finden Sie hier: 10 minute (wx)Maxima Tutorial (German)