Inhaltsverzeichnis
Stack (Maxima)
Mathematische Aufgaben mit Moodle/Stack
STACK (the System for Teaching and Assessment using a Computer algebra Kernel) ermöglicht es Ihnen, mathematische Fragestellungen in Moodle-Tests zu realisieren. Das Plugin nutzt das Computeralgebrasystem „Maxima“, um mathematische Eigenschaften der eingegebenen Antworten bzw. Ausdrücke zu ermitteln und diese zu bewerten.
Hilfen zur Einarbeitung
Einen Vortrag (Dauer: 36:09), in dem STACK von anderen Aufgabentypen, wie z.B. Multiple Choice, abgegrenzt und ein Überblick über die Möglichkeiten von STACK gegeben wird, finden Sie hier:
https://www.rubel.rub.de/news/vortrag-vom-1692015-online-intelligente-rechenaufgaben-mit-stack-moodle
Sehr hilfreich ist auch der Moodle-Kurs, der in der Ruhr-Universität Bochum von Herrn Kallweit und seinem Team erstellt wurde:
https://moodle.ruhr-uni-bochum.de/m/course/view.php?id=13674
Dort gibt es viele Videos und Beispiele zum Ausprobieren.
Wenn ein Benutzeraccount unter
https://moodle.ruhr-uni-bochum.de/m/login/signup.php
erstellt wurde, kann man in dem Kurs sogar die vorgestellten Beispiele im XML-Format herunterladen.
In diesem Video können Sie sich einen Überblick über die Erstellung von Aufgaben in STACK verschaffen:
Im Folgenden wird zur Einführung ein Teil der Möglichkeiten dieses Aufgabentyps beschrieben. Ergänzende Informationen können Sie den entsprechenden Dokumentationen entnehmen:
Maxima Manuals:
http://maxima.sourceforge.net/docs/manual/de/maxima.html (deutsch)
http://michel.gosse.free.fr/documentation/fichiers/maxima.pdf (englisch)
Offizielle Plugin-Seite:
https://moodle.org/plugins/qtype_stack (englisch)
Weiterer, durch Videos unterstützter Kurs „Authoring quick start“ (besteht z.Zt. aus acht Einheiten) von den Entwicklern von STACK:
https://github.com/maths/moodle-qtype_stack/blob/master/doc/en/Authoring/Authoring_quick_start.md (Startseite, englisch)
Die Videos sind unter z.B. https://www.youtube.com/watch?time_continue=223&v=cpwo-D6EUgA&feature=emb_logo direkt bei YouTube zu finden
Grundlagen zum Stack Fragetyp
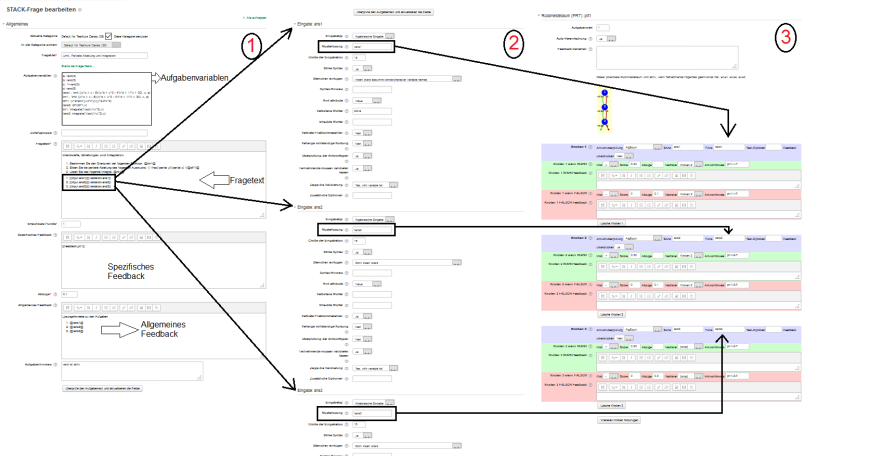
Im Folgenden wird die grundlegende Struktur einer Stack-Frage beschrieben. Im ersten Bereich werden die Aufgabenvariablen (ans1,ans2,…,ansn) definiert, die konkrete Frage/Aufgabe formuliert, die Art und die Anzahl der Eingabe/Input-Felder (Textfelder, Matrizen, etc.) festgelegt und das allgemeine Feedback (z.B. Lösungshinweise) vorbereitet. Im zweiten Bereich werden die spezifischen Eigenschaften der Eingabefelder (Platzhalter, Typ des Feldes, Musterantwort, etc.) festgelegt. Dabei können bzw. sollten Sie in dem jeweiligen Feld für die Musterlösung die im ersten Bereich definierten Aufgabenvariablen (tans1,tans2,…,tansn) verwenden. Im dritten Bereich wird zum Schluss die Auswertungslogik erstellt. Dazu werden sogenannte „Potential-Response-Trees“ (PRT, Rückmeldebäume) erstellt (siehe Potential-Response-Trees).
Aufbau der Stack Fragen
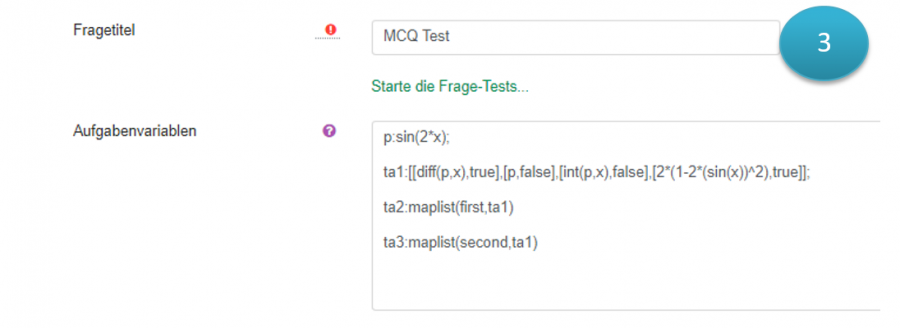
Fragetitel
Geben Sie hier einen aussagekräftigen Titel, wie z.B. „Nullstellenbestimmung - 1“, ein.
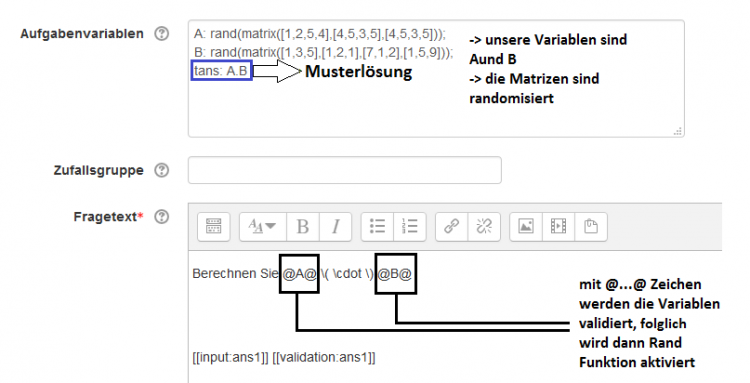
Aufgabenvariablen
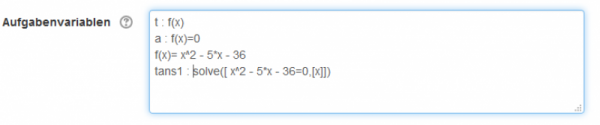
Im Bereich „Aufgabenvariablen“ können Variablen und entsprechende Wertzuweisungen und mathematische Ausdrücke vorbereitet werden.
variablenname : Ausdruck
t : 2 // der Variable t wird der Wert 2 zugewiesen a : f(x)=x^2 // Abbildung einer Funktion b : diff(x^2,x) // differenziere x^2 nach x c : diff(a,x) // alternativ: differenziere a nach x d : rand(15) // Zufallszahlen von 0 bis 14
Siehe dazu auch: Arbeiten mit Zufallszahlen, Maxima Dokumentation, Arbeiten mit Funktionen
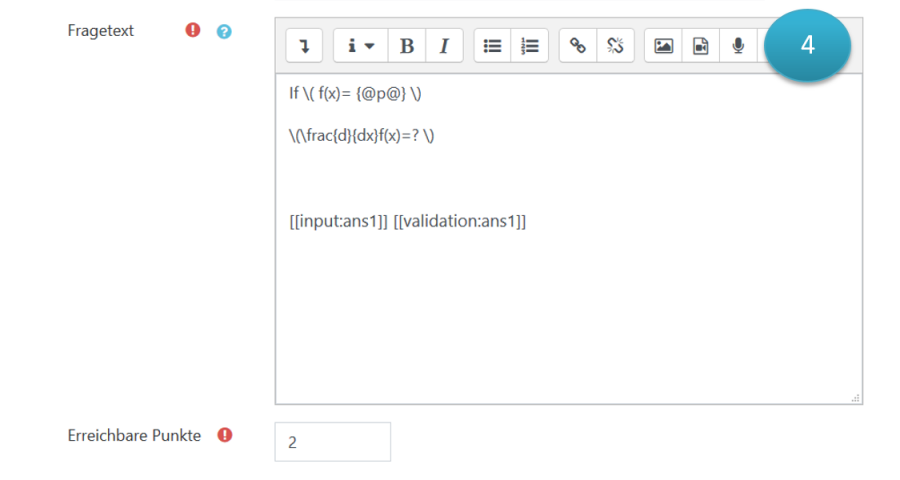
Fragetext
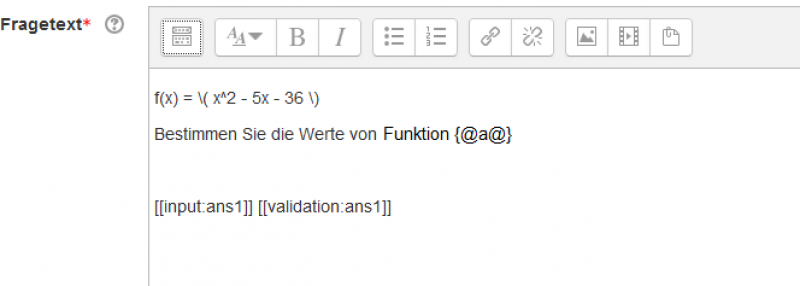
In diesen Abschnitt erfolgt die konkrete Aufbereitung bzw. Formulierung der Frage/Aufgabe. Bitte beachten Sie, dass sich die Syntax der Stackausdrücke verändert hat! @...@ wird zu {@...@}
Mit Hilfe von Medieninhalten (Bildern, Videos) und LaTeX stehen Ihnen einige Möglichkeiten zur Formulierung von komplexen Aufgaben zur Verfügung. Sie können die erweiterten Features im Menü des WYSIWYG-Editors nutzen, um ihre Aufgaben z.B. mit LaTeX-Ausdrücken zu formulieren:
- Klicken Sie dazu auf das Icon „mehr Symbole anzeigen“
- Öffnen Sie den Gleichungseditor
Eingabefelder verwenden / erweitern
Im Aufgabentyp Moodle Stack wird das erste „Eingabefeld“ automatisch beim Anlegen einer Aufgabe erstellt. Wenn zusätzliche Eingabefelder benötigt werden, können Sie beliebig viele Eingabefelder nach dem folgenden Muster
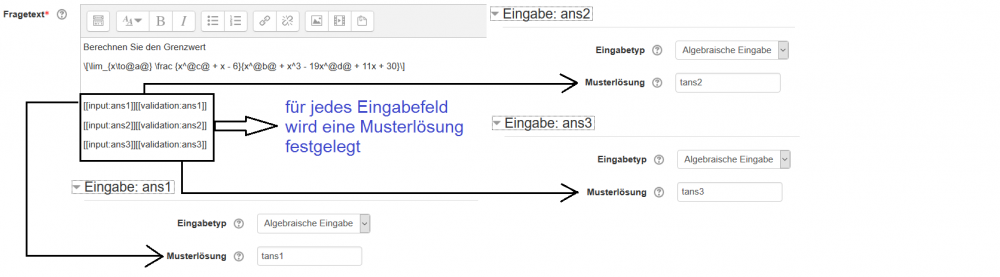
[[input:ans2]] [[validation: ans2]] [[input:ans3]] [[validation: ans3]] ... [[input:ansx]] [[validation: ansx]]
in einer Aufgabe hinzufügen (nach jedem Hinzufügen eines neuen Eingabefelds muss die Frage aktualisiert werden). Für jedes Eingabefeld muss eine Musterlösung (z.B. Aufgabenvariable oder Ausdruck) festgelegt werden.
Allgemeines Feedback
Beim allgemeinen Feedback handelt es sich um eine Ergänzung der Musterlösung. Dieses Feedback wird allen Studierenden nach dem Ende des Versuchs angezeigt, unabhängig davon, welche Antworten sie gegeben haben. In diesem Feld können die Aufgabenvariablen verwendet werden, allerdings nicht die Eingaben der Studierenden wie ans1, ans2 usw.
Eingabetypen und Optionen zu den Eingabefeldern
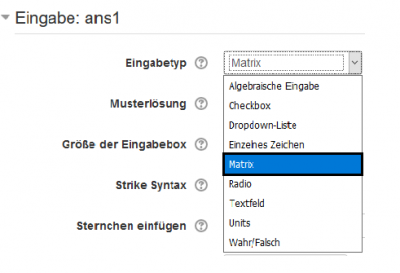
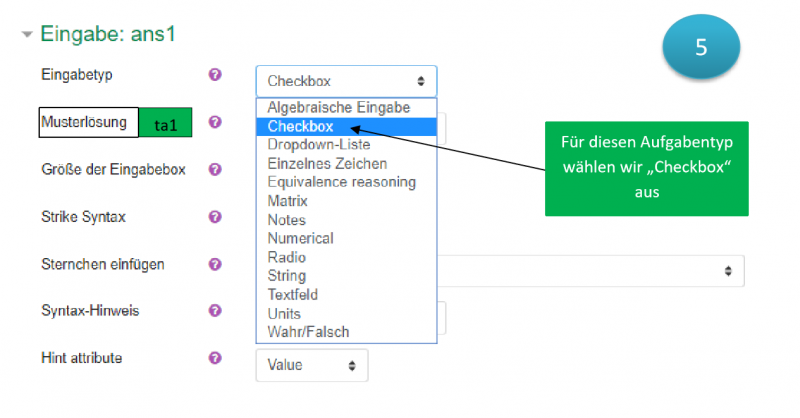
Zu jedem Eingabefeld muss mindestens der Eingabetyp sowie die Musterlösung angegeben werden.
Als Eingabetyp stehen folgende Optionen zur Auswahl:
- Algebraische Eingabe
- Hier kann ein algebraischer Ausdruck, also eine Zahl oder eine Funktion, auch Variablen von den Studierenden eingegeben werden.
- Anmerkung
- In diesem Eingabefeld können die Studierenden etwas Beliebiges für ihre eigenen Notizen schreiben. Es wird nicht ausgewertet, sondern das CAS bekommt immer den Wert „true“ übermittelt, egal was in dem Feld steht.
- Checkbox
- Für MC-Aufgaben (Multiple Choice)
- Dropdown-Liste
- Für MC-Aufgaben
- Einheiten
- Wird als Eingabetyp Einheiten gewählt, so kann die Antwort der Studierenden auf die korrekte Verwendung von Einheiten überprüft werden, zu beachten ist hierbei, dass STACK nur SI-Einheiten unterstützt. Um eine Antwort auch hinsichtlich der Einheit zu prüfen, muss als Musterlösung die vollständige Antwort inklusive Einheiten eingegeben werden. Außerdem muss im PRT eine entsprechende Antwortüberprüfung (mit „Units“ beginnend) gewählt werden (beispielsweise UnitsAbsolute). Die korrekte TeacherAnswer (TAns) muss ebenfalls inklusive Einheit angegeben werden. In den Antwortoptionen muss außerdem der Toleranzbereich für die Antwort eingegeben werden, der sich auf den numerischen Teil der Antwort bezieht. (Die Eingabe 0.1 für die Antwortüberprüfung UnitsAbsolute bedeutet dabei, dass TAns+/- 0,1 als richtige Antwort akzeptiert wird).
(Beitrag von: Yvonne Wolf, HS Hannover)
- Einzelnes Zeichen
- Wird nur selten benutzt. Hiermit kann bei MC-Aufgaben die Gelegenheit gegeben werden, z.B. „d“ als mögliche Lösung einzugeben.
- Equivalence Reasoning
- Matrix
- Numerisch
- Bei diesem Eingabetyp muss eine Zahl eingegeben werden. Im Unterschied zum Eingabetypen „Algebraische Eingabe“ können hier von den Studierenden keine Variablen eingegeben werden.
- Radiobuttons
- Für MC-Aufgaben
- Textfeld
- Wahr/Falsch
- Zeichenkette
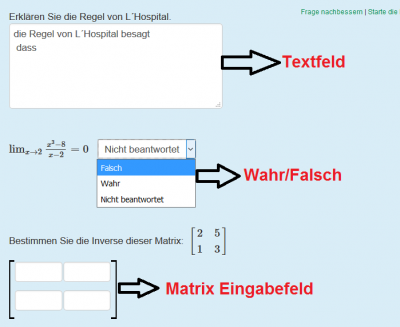
Standardmäßig ist hier die algebraische Eingabe eingestellt.
Im Bild werden die Optionen „Textfeld“, „Wahr/Falsch“ und „Matrix“ gezeigt.
Weiterführende Informationen (englisch):
Eingabetypen allgemein: https://github.com/maths/moodle-qtype_stack/blob/master/doc/en/Authoring/Inputs.md
Einheiten: https://github.com/maths/moodle-qtype_stack/blob/master/doc/en/Authoring/Units.md
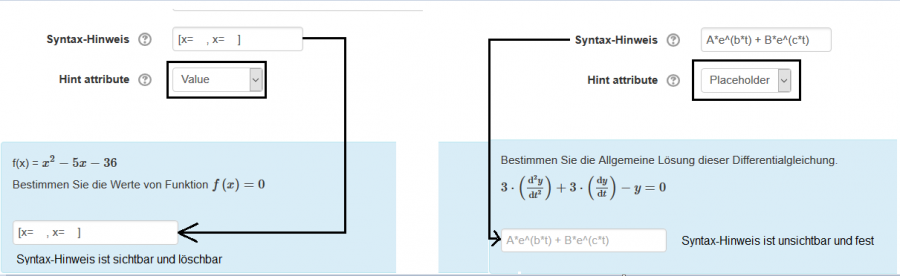
Syntax Hint oder Syntax-Hinweise sind Platzhalter innerhalb der Eingabefelder, die Ihren Studenten eine Vorlage liefern, wie ein Term eingeben werden soll (z.B. sqrt, [x=..,x=..]).
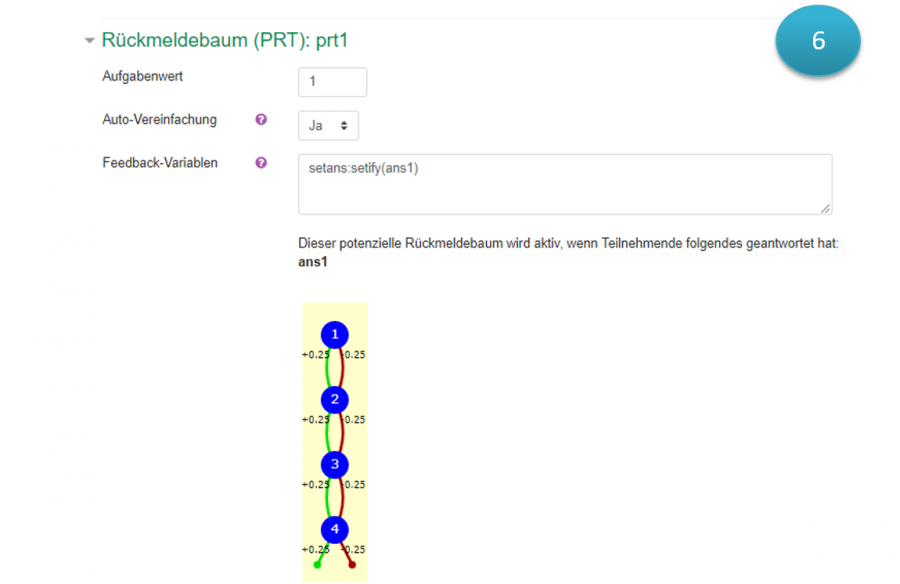
Rückmeldebaum (PRT)
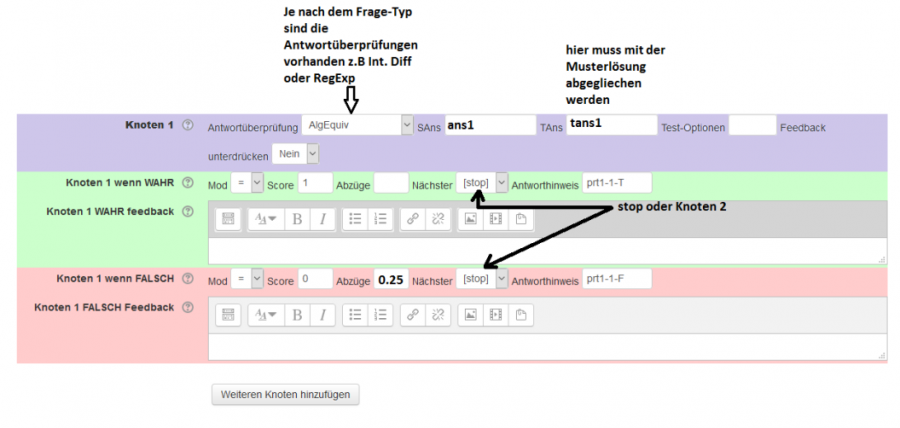
Die Potential Response Trees (PRT) sind binäre Baumstrukturen und werden zum Aufbau einer Auswertungslogik der Aufgabe verwendet. Dabei werden Antworten bzw. die Eingaben eines Studenten mit einem math. Ausdruck (z.B. der „Musterlösung“) verglichen.
ResponseTrees können flexibel aufgebaut werden. Die Knoten können (nachdem sie angelegt wurden) miteinander verknüpft werden (z.B. Folgefehler-Szenarien). Um Knoten hinzuzufügen, müssen Sie lediglich auf den Button „weitere Knoten hinzufügen“ klicken.
- wie werden Knoten und Punkte verarbeitet (Score, Abzüge):
Die Anzahl der maximal zu erreichenden Punkte (Score) beträgt 1,00. Wenn die Teilnehmenden falsche Antwort gegeben haben, werden 0.25 Punkte abgezogen.
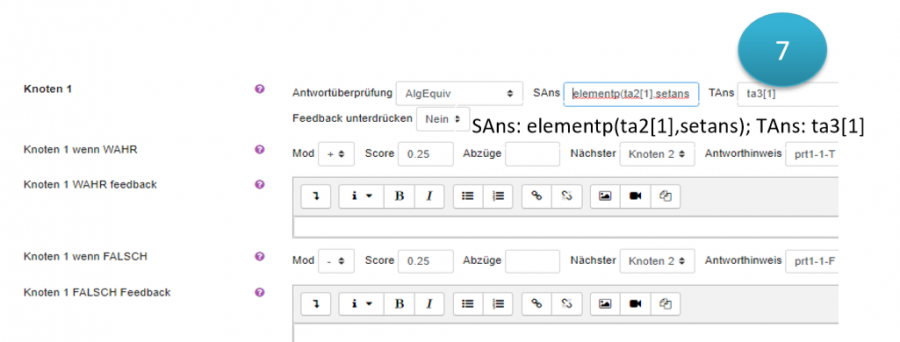
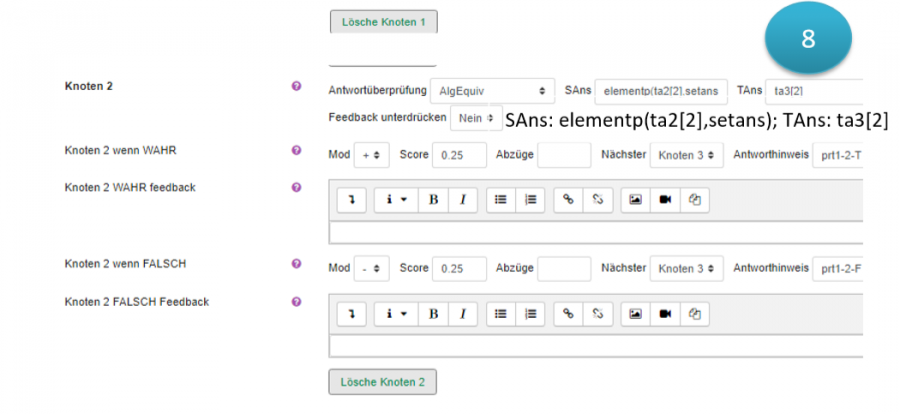
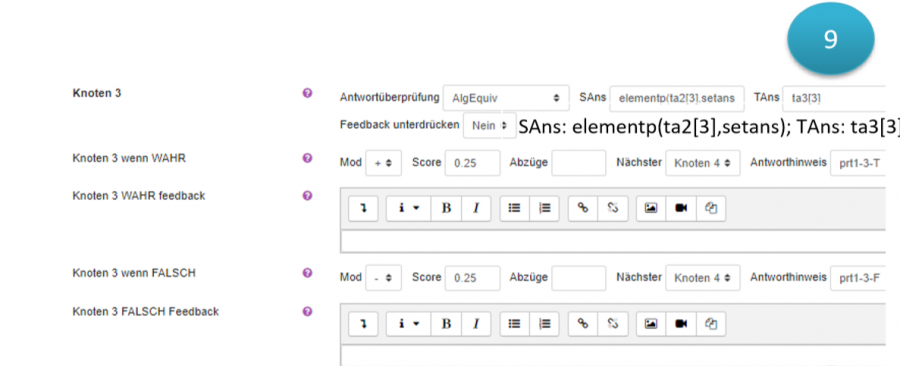
- wie funktioniert die Anwortüberprüfung
Eine Antwortüberprüfung(Answer test) wird verwendet um zwei Ausdrücke zu vergleichen und um festzustellen ob sie einige Kriterien erfüllen.
Hinweise zur Antwortüberprüfung
NumDecPlaces
NumDecPlaces prüft, ob die Antwort des Schülers die des Lehrers entspricht und auf die vorgegebene Anzahl von Dezimalstellen geschrieben wird. Die Option, die eine positive ganze Zahl sein muss, gibt die Anzahl der Stellen an, die auf das Dezimaltrennzeichen folgen. Beachten Sie, dass nachfolgende Nullen erforderlich sind, d.h., bei einer Vorgabe von zwei Dezimalstellen, müssen Sie 12.30 und nicht nur 12.3 schreiben. Der Test rundet die Zahlen auf die angegebene Anzahl von Dezimalstellen, bevor versucht wird, eine Äquivalenz herzustellen.
Beispiel: Wir möchten für die Frage eine Antwort mit 3 Dezimalstellen haben. Dies bedeutet, dass die Option den Wert 3 enthalten sollte. Sei nun 15.3468 eine möglich Antwort. Dieser Test rundet die Zahl 15.3468 auf 15.347, da 3 Dezimalstellen gewünscht werden.
NumRelative & NumAbsolute
Die Option für diese Tests ist eine Toleranz. Die Standardtoleranz beträgt 0,05.
Relative: Tests whether abs(sa-ta) <= opt * abs(ta) Absolute: Tests whether abs(sa-ta) < opt
NumRelative und NumAbsolute können auch Listen und Sets akzeptieren. Elemente werden automatisch in Floats umgewandelt und vereinfacht (z.B Ev(Float(ex),simp)) und mit der Antwort des Lehrers unter Verwendung des entsprechenden numerischen Tests und der entsprechenden Genauigkeit verglichen. Es muss eine einheitliche Genauigkeit verwendet werden. Bei Listen ist die Reihenfolge wichtig, bei Sets jedoch nicht. Überprüfung, ob zwei Sätze ungefähr gleich sind, ist ein interessantes mathematisches Problem…
Grundlagen
Zufallszahlen
Eine Zufallszahl von 0 - 98 oder eine Zufallszahl aus der Menge {1,2,3,4}
z1 : rand(99) z2 : rand([1,2,3,4])
Eine Zufallszahl mit den folgenden möglichen Werten: Min: 2, Max: 25, Inkrement: 3
z3 : rand_with_step(2,25,3)
oder eine Zufallszahl ohne den Wert von z3
z4 : rand_with_prohib(2,8,[z3])
Eine Liste kann wie folgt erstellt werden : [a,b,c]
Konstanten
e // Eulersche Zahl pi // π Kreiszahl infinity // ∞ komplex unendlich inf // positiv unendlich minf // negativ unendlich i // imaginäre Einheit i(in der Elektrotechnik oft bezeichnet mit j) phi // Goldener Schnitt φ=(1+√5)/2
Für mehr Informationen klicken Sie bitte auf den folgenden Link: Mathematische Konstanten
Trigonometrische Funktionen
sin(x), cos(x), tan(x) und cot(x)
und deren Inverse:
asin(x), acos(x), atan(x) und acot(x)
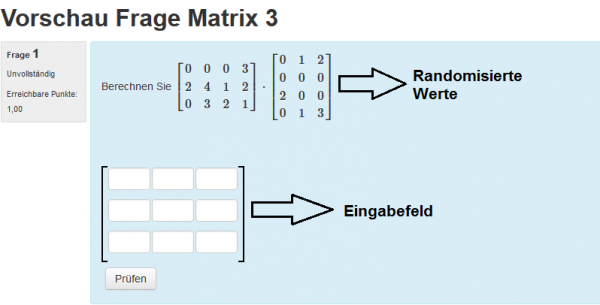
Matrizen
- Definieren Sie Ihre Aufgabenvariablen
A : rand(matrix([1,2,4,3],[4,5,3,5],[4,5,3,5])) // Matrix A B : rand(matrix([1,3,5],[1,2,1],[7,1,2],[1,5,9])) // Matrix B tans : A.B // Matrixmultiplikation
Funktionen und Funktionstypen
Ausdrücke automatisch auswerten
Die Informationen zu den möglichen Funktionen →http://maxima.sourceforge.net/docs/manual/maxima.html
ev(Evaluate)
f1: x+3*y+z; tans1: ev(f1,x=2,y=1,z=1); tans1=5
solve / linsolve
Beispiel 1
f: x^2-2*x+1=0 tans1:solve([f],[x])
Beispiel 2 (Lineargleichungen)
f1: x+3*y+z=9 f2: x-8*y+6*z=17 f3: 2*x+7*y-9*z=22 tans1:linsolve([f1,f2,f3],[x,y,z])
Für mehr Informationen sehen Sie auch Maxima-Equations
limit
s: (1+1/x)^x tans1:limit(s,x,infinity)
ode2 (Differentialgleichungen)
Beispiel:
dg1 : 'diff(y,x,2)-3*'diff(y,x)-4*y=0
Dabei bedeutet das Symbol < ' > lediglich, dass Maxima den Ausdruck nicht auswertet. Das ist z.B. dann praktisch, wenn man in diesem Beispiel die Funktion nicht tatsächlich differenzieren, aber eben entsprechend in diesem Kontext $ \frac{dy}{dx}$ ausgeben möchte.
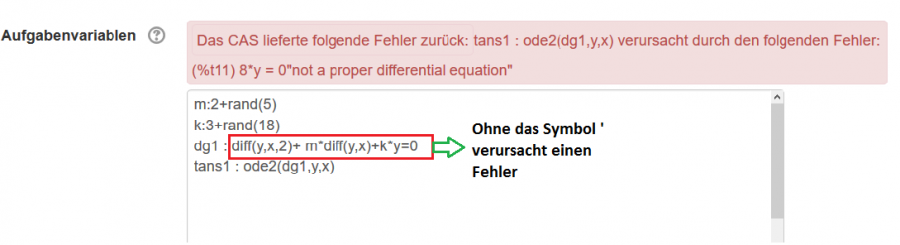
Befehle zur Lösung dieser Differentialgleichung:
tans1:ode2(dg1,y,x)
Siehe auch: Differential Equations
plot
Beispiel:
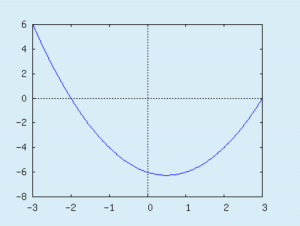
Mit Randomisierung der Werte für den Plot:
a: 1+rand(5) b: 3+rand(25) d: -1*rand(5) e: 1+rand(5) t: x^2-a*x+b tans1: plot([t],[x,d,e])
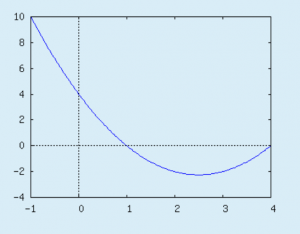
Ein Diagramm mit mehreren Plot-Optionen (grid, color, labels, usw.):
a: 1+rand(5) b: 3+rand(25) d: -1*rand(5) e: 1+rand(5) t1: x^2-a*x+b t2: x^2 + b*x-12*a tans1: plot([t1,t2],[x,d,e],[xlabel,"x-Axis"],[ylabel,"y-Axis"],[color,blue,red],[axes,true],[box,false],grid2d)
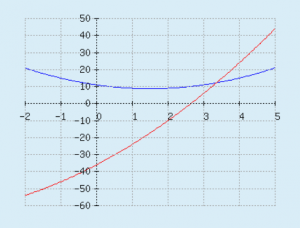
Beachte: Die Maxima Funktionen plot2d() und plot3d() wurden für STACK aus Sicherheitsgründen in plot() gekapselt und funktionieren somit auch nur ausschließlich als plot().
Videos zur Hilfe für Erstellung der bestimmten Aufgabentypen
Matrixaufgabe
Matrixaufgabe mit randomisierten Werten
Lineare Gleichungen mit randomisierten Werten
Lineare Differentialgleichung mit konstanten Koeffizienten